Calculation methods of geographical complexity
The formula for shannon entropy is as follows:
\[ H(X) = - \sum_{i=1}^{n} p(x_i) \log_b p(x_i) \]
Where \(H(X)\) is entropy of the random variable \(X\), \(p(x_i)\) is probability of the random variable \(X\) taking the value \(x_i\), \(n\)is number of possible values that \(X\) can take, \(b\) is the base of the logarithm, which can be 2 (for bits), \(e\) (natural logarithm, for nats), or 10 (for dits).
The spatial variance is calculated as:
\[ \Gamma = \frac{\sum_i \sum_{j \neq i} \omega_{ij}\frac{(y_i-y_j)^2}{2}}{\sum_i \sum_{j \neq i} \omega_{ij}} \]
where \(\omega_{ij}\) is the weight between \(i\)-th location and \(j\)-th location; \(y_i\) and \(y_j\) are the dependent variable values at the \(i\)-th and \(j\)-th locations respectively.
The geographical configuration similarity is calculated as:
\[ S({\bf u}_{\alpha},{\bf v}_{\beta})=min\{E_{i}(e_{i}({\bf u}_{\alpha}),e_{i}({\bf v}_{\beta}))\} \]
\[ E_{i}({\bf u}_{\alpha},{\bf v}_{\beta})=\exp\left(-{\frac{\left(e_{i}({\bf u}_{\alpha})-e_{i}({\bf v}_{\beta})\right)^{2}}{2\left(\sigma^{2}/\delta({\bf v}_{\beta})\right)^{2}}}\right) \]
\[ \delta({\bf u}_{\alpha},{\bf v})=\sqrt{\frac{\sum_{\beta=1}^{n}(e({\bf u}_{\alpha})-e({\bf v}_{\beta}))^{2}}{n}} \]
Considering the geographical complexity with spatial local dependencies
The formula for geocomplexity which uses local moran measure method is
\[ \rho_i = -\frac{1}{m} Z_i \sum\limits_{j=1}^m W_{ij} Z_j -\frac{1}{m} \sum\limits_{j=1}^m W_{ij} Z_j \frac{1}{V_{k}}\sum\limits_{k=1}^n W_{jk} W_{ik} Z_k \]
The formula for geocomplexity which uses spatial fluctuation measure method is
\[ \rho_i = Spatial\_Variance(z_i,z_j) \]
The formula for geocomplexity which uses shannon entropy measure method is
\[ \rho_i = Shannon\_Entropy(Z_i,Z_j) \]
Cases for computing geographical complexity
Geographical Complexity of Individual Variables
library(sf)
library(geocomplexity)
library(ggplot2)
library(viridis)
library(patchwork)
econineq = sf::read_sf(system.file('extdata/econineq.gpkg',package = 'geocomplexity'))
gc = geocd_vector(econineq)
gc
## Simple feature collection with 333 features and 9 fields
## Geometry type: MULTIPOLYGON
## Dimension: XY
## Bounding box: xmin: 112.9211 ymin: -43.63311 xmax: 153.6299 ymax: -9.223927
## Geodetic CRS: GDA94
## # A tibble: 333 × 10
## GC_Gini GC_Induscale GC_IT GC_Income GC_Sexrat GC_Houseown GC_Indemp GC_Indcom GC_Hiedu
## <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl>
## 1 0.899 0.922 0.945 0.952 0.845 0.906 0.858 0.889 0.924
## 2 0.895 0.919 0.849 0.925 0.770 0.825 0.853 0.872 0.877
## 3 0.922 0.919 0.861 0.914 0.729 0.759 0.888 0.911 0.877
## 4 0.921 0.919 0.834 0.949 0.775 0.807 0.892 0.911 0.863
## 5 0.850 0.924 0.830 0.930 0.778 0.889 0.863 0.886 0.843
## 6 0.944 0.920 0.873 0.956 0.782 0.856 0.865 0.929 0.858
## 7 0.910 0.921 0.891 0.957 0.799 0.865 0.809 0.912 0.834
## 8 0.924 0.919 0.817 0.938 0.810 0.834 0.910 0.911 0.867
## 9 0.929 0.919 0.663 0.901 0.768 0.837 0.911 0.914 0.773
## 10 0.918 0.919 0.841 0.957 0.758 0.863 0.927 0.918 0.823
## # ℹ 323 more rows
## # ℹ 1 more variable: geometry <MULTIPOLYGON [°]>
plot_geocd = \(.x){
ggplot(gc) +
geom_sf(aes(fill = gc[,.x,drop = TRUE])) +
scale_fill_viridis(option = "mako", direction = -1,name = "") +
theme_bw()
}
fig1 = names(gc)[1:9] %>%
purrr::map(plot_geocd) %>%
wrap_plots(ncol = 3, byrow = TRUE,
guides = "collect") +
plot_annotation(tag_levels = 'a',
tag_prefix = '(',
tag_suffix = ')',
tag_sep = '',
theme = theme(plot.tag = element_text(family = "serif"),
plot.tag.position = "topleft"))
fig1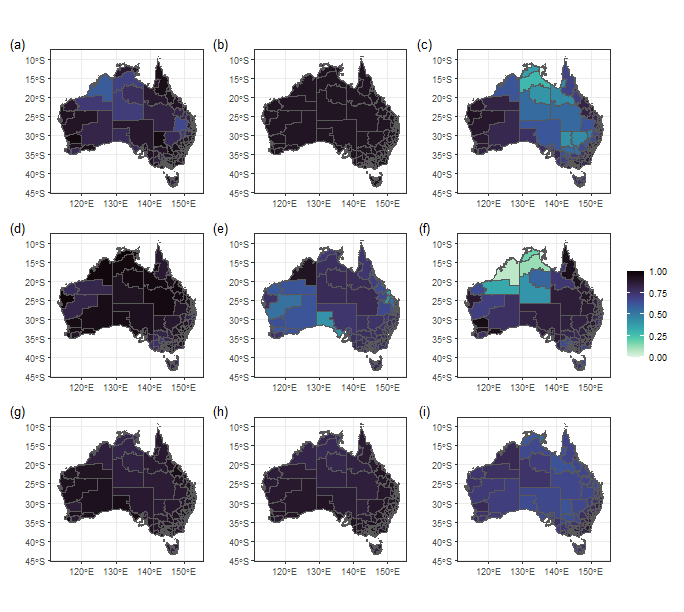
Geographical Complexity of Multiple Variables
gc_multi = geocs_vector(dplyr::select(econineq,-Gini))
gc_multi
## Simple feature collection with 333 features and 1 field
## Geometry type: MULTIPOLYGON
## Dimension: XY
## Bounding box: xmin: 112.9211 ymin: -43.63311 xmax: 153.6299 ymax: -9.223927
## Geodetic CRS: GDA94
## # A tibble: 333 × 2
## GC geometry
## <dbl> <MULTIPOLYGON [°]>
## 1 0.210 (((149.979 -35.50246, 149.9774 -35.49025, 149.9987 -35.47874, 150.0059 -35.46051, 15…
## 2 0.155 (((148.8041 -35.71402, 148.782 -35.73665, 148.7666 -35.70281, 148.7535 -35.6878, 148…
## 3 0.147 (((150.3754 -35.56524, 150.3725 -35.55018, 150.36 -35.53485, 150.2819 -35.5241, 150.…
## 4 0.213 (((149.0114 -33.93276, 149.0057 -33.94396, 149.013 -33.96863, 149.0114 -33.98291, 14…
## 5 0.184 (((147.7137 -34.16162, 147.7126 -34.17681, 147.728 -34.18633, 147.7443 -34.1801, 147…
## 6 0.353 (((151.485 -33.39868, 151.4645 -33.39985, 151.4539 -33.37713, 151.4415 -33.38963, 15…
## 7 0.307 (((151.485 -33.39868, 151.4839 -33.38366, 151.5049 -33.35415, 151.499 -33.33902, 151…
## 8 0.214 (((149.323 -33.05916, 149.3147 -33.10072, 149.3226 -33.1168, 149.3171 -33.14661, 149…
## 9 0.133 (((149.1264 -33.86642, 149.1349 -33.85089, 149.1314 -33.83058, 149.1155 -33.79723, 1…
## 10 0.180 (((150.5587 -32.75774, 150.5411 -32.75426, 150.527 -32.75969, 150.5182 -32.74934, 15…
## # ℹ 323 more rows
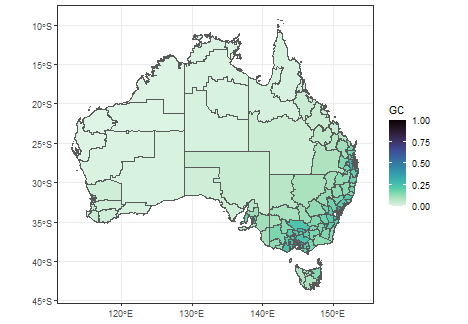
fig2 = ggplot(gc_multi) +
geom_sf(aes(fill = GC)) +
scale_fill_viridis(option = "mako", direction = -1) +
theme_bw()
fig2